5  Trajectory with wind

library(GeoPressureR)
library(ggplot2)

In this second chapter of the advanced tutorial, we explore how to model the trajectory of the Great Reed Warbler using wind data.

tag <- tag_create(
  "18LX",
  crop_start = "2017-06-20",
  crop_end = "2018-05-02",
  quiet = TRUE
) |>
  tag_label(quiet = TRUE) |>
  tag_set_map(
    extent = c(-16, 23, 0, 50),
    scale = 4,
    known = data.frame(
      stap_id = 1,
      known_lat = 48.9,
      known_lon = 17.05
    )
  ) |>
  geopressure_map(quiet = TRUE) |>
  twilight_create() |>
  twilight_label_read() |>
  geolight_map()

Wind can significantly influence a bird’s movement, explaining up to 50% of the displacement! Accounting for wind allows us to estimate the airspeed of each transition rather than groundspeed. As such, the movement model can be defined as the probability of a bird’s airspeed, which is much more constrained and precise. This approach is presented in detail in section 2.2.4 of Nussbaumer et al. (2023).

5.1 Download wind data

Wind data is available at high resolution (1hr, 0.25°, 37 pressure level) on ERA5 hourly data on pressure levels (Copernicus Climate Change Service 2018). This data is easily accessible through the ecmwfr package.

Caution

Learn how to set-up your ECMWF account to be able to download ERA5 data on the GeoPressureTemplate/Download Wind page.

As the flights tend to be of short duration, we suggest downloading a file for each flight. This can be done automatically with tag_download_wind(), which uses wf_request_batch() to make all the requests in parallel.

tag_download_wind(
  tag,
  variable = c("u_component_of_wind", "v_component_of_wind", "temperature")
)

You can monitor the requests at [https://cds.climate.copernicus.eu/requests]. The files are downloaded in data/wind/

Note

In addition to the two required wind variables, we also downloaded the temperature data during the flights. This will later allow us to retrieve temperature data at the exact location of the bird during the flight. See tag_download_wind() documentation for more information on the available variables.

Tip

In case you have a lot of tracks for which you need to download wind data and don’t want to block your console, you might consider using an RStudio background job, which can be easily called with the job package:

job::job({
  tag_download_wind(tag)
})

5.2 Create graph

Similar to the example of the Swainson’s Warbler in the basic tutorial, we first need to create the trellis graph:

graph <- graph_create(tag, quiet = TRUE)

5.3 Add wind to graph

We then compute the average windspeed experienced by the bird for each edge of the graph. This process can be quite long as we need to interpolate the position of the bird along its flight on a 4D grid (latitude-longitude-pressure level-time).

We then compute the airspeed based on this windspeed and the known groundspeed. All of these are stored as complex values with the real part representing the E-W component and the imaginary part corresponding to the N-S component.

graph <- graph_add_wind(graph, pressure = tag$pressure, quiet = TRUE)

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 17
ℹ Date: 2017-08-31 18:00:00
ℹ Pressure: 1010 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 510 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 17
ℹ Date: 2017-08-31 19:00:00
ℹ Pressure: 924 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 424 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 17
ℹ Date: 2017-08-31 20:00:00
ℹ Pressure: 964 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 464 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 17
ℹ Date: 2017-08-31 21:00:00
ℹ Pressure: 974 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 474 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 17
ℹ Date: 2017-08-31 22:00:00
ℹ Pressure: 984 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 484 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 17
ℹ Date: 2017-08-31 23:00:00
ℹ Pressure: 923 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 423 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 17
ℹ Date: 2017-09-01 00:00:00
ℹ Pressure: 806 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 306 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 8 of 17
ℹ Date: 2017-09-01 01:00:00
ℹ Pressure: 720 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 220 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 9 of 17
ℹ Date: 2017-09-01 02:00:00
ℹ Pressure: 660 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 160 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 10 of 17
ℹ Date: 2017-09-01 03:00:00
ℹ Pressure: 722 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 222 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 11 of 17
ℹ Date: 2017-09-01 04:00:00
ℹ Pressure: 696 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 196 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 12 of 17
ℹ Date: 2017-09-01 05:00:00
ℹ Pressure: 710 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 210 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 13 of 17
ℹ Date: 2017-09-01 06:00:00
ℹ Pressure: 582 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 82 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 14 of 17
ℹ Date: 2017-09-01 07:00:00
ℹ Pressure: 515 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 15 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 15 of 17
ℹ Date: 2017-09-01 08:00:00
ℹ Pressure: 580 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 80 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 16 of 17
ℹ Date: 2017-09-01 09:00:00
ℹ Pressure: 857 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 357 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 7
ℹ Flight index: 1 of 1
ℹ Time index: 17 of 17
ℹ Date: 2017-09-01 10:00:00
ℹ Pressure: 932 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 432 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 17
ℹ Date: 2017-09-01 18:00:00
ℹ Pressure: 924 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 324 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 17
ℹ Date: 2017-09-01 19:00:00
ℹ Pressure: 921 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 321 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 17
ℹ Date: 2017-09-01 20:00:00
ℹ Pressure: 837 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 237 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 17
ℹ Date: 2017-09-01 21:00:00
ℹ Pressure: 736 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 136 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 17
ℹ Date: 2017-09-01 22:00:00
ℹ Pressure: 636 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 36 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 17
ℹ Date: 2017-09-01 23:00:00
ℹ Pressure: 756 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 156 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 17
ℹ Date: 2017-09-02 00:00:00
ℹ Pressure: 799 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 199 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 8 of 17
ℹ Date: 2017-09-02 01:00:00
ℹ Pressure: 715 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 115 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 9 of 17
ℹ Date: 2017-09-02 02:00:00
ℹ Pressure: 764 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 164 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 10 of 17
ℹ Date: 2017-09-02 03:00:00
ℹ Pressure: 686 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 86 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 11 of 17
ℹ Date: 2017-09-02 04:00:00
ℹ Pressure: 705 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 105 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 12 of 17
ℹ Date: 2017-09-02 05:00:00
ℹ Pressure: 778 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 178 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 13 of 17
ℹ Date: 2017-09-02 06:00:00
ℹ Pressure: 792 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 192 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 14 of 17
ℹ Date: 2017-09-02 07:00:00
ℹ Pressure: 823 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 223 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 15 of 17
ℹ Date: 2017-09-02 08:00:00
ℹ Pressure: 819 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 219 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 16 of 17
ℹ Date: 2017-09-02 09:00:00
ℹ Pressure: 946 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 346 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 8
ℹ Flight index: 1 of 1
ℹ Time index: 17 of 17
ℹ Date: 2017-09-02 10:00:00
ℹ Pressure: 947 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 347 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 9
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 10
ℹ Date: 2017-09-04 20:00:00
ℹ Pressure: 943 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 168 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 9
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 10
ℹ Date: 2017-09-04 21:00:00
ℹ Pressure: 865 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 90 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 9
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 10
ℹ Date: 2017-09-04 22:00:00
ℹ Pressure: 818 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 43 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 9
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 10
ℹ Date: 2017-09-04 23:00:00
ℹ Pressure: 796 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 21 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 9
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 10
ℹ Date: 2017-09-05 00:00:00
ℹ Pressure: 849 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 74 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 9
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 10
ℹ Date: 2017-09-05 01:00:00
ℹ Pressure: 783 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 8 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 9
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 10
ℹ Date: 2017-09-05 02:00:00
ℹ Pressure: 796 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 21 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 9
ℹ Flight index: 1 of 1
ℹ Time index: 8 of 10
ℹ Date: 2017-09-05 03:00:00
ℹ Pressure: 787 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 12 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 9
ℹ Flight index: 1 of 1
ℹ Time index: 9 of 10
ℹ Date: 2017-09-05 04:00:00
ℹ Pressure: 834 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 59 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 9
ℹ Flight index: 1 of 1
ℹ Time index: 10 of 10
ℹ Date: 2017-09-05 05:00:00
ℹ Pressure: 977 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 202 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 10
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 11
ℹ Date: 2017-09-06 19:00:00
ℹ Pressure: 976 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 276 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 10
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 11
ℹ Date: 2017-09-06 20:00:00
ℹ Pressure: 937 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 237 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 10
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 11
ℹ Date: 2017-09-06 21:00:00
ℹ Pressure: 882 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 182 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 10
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 11
ℹ Date: 2017-09-06 22:00:00
ℹ Pressure: 752 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 52 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 10
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 11
ℹ Date: 2017-09-06 23:00:00
ℹ Pressure: 797 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 97 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 10
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 11
ℹ Date: 2017-09-07 00:00:00
ℹ Pressure: 841 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 141 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 10
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 11
ℹ Date: 2017-09-07 01:00:00
ℹ Pressure: 801 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 101 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 10
ℹ Flight index: 1 of 1
ℹ Time index: 8 of 11
ℹ Date: 2017-09-07 02:00:00
ℹ Pressure: 831 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 131 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 10
ℹ Flight index: 1 of 1
ℹ Time index: 9 of 11
ℹ Date: 2017-09-07 03:00:00
ℹ Pressure: 830 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 130 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 10
ℹ Flight index: 1 of 1
ℹ Time index: 10 of 11
ℹ Date: 2017-09-07 04:00:00
ℹ Pressure: 833 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 133 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 10
ℹ Flight index: 1 of 1
ℹ Time index: 11 of 11
ℹ Date: 2017-09-07 05:00:00
ℹ Pressure: 980 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 280 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 11
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 8
ℹ Date: 2017-09-09 19:00:00
ℹ Pressure: 981 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 156 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 11
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 8
ℹ Date: 2017-09-09 20:00:00
ℹ Pressure: 978 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 153 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 11
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 8
ℹ Date: 2017-09-09 21:00:00
ℹ Pressure: 865 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 40 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 11
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 8
ℹ Date: 2017-09-09 22:00:00
ℹ Pressure: 854 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 29 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 11
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 8
ℹ Date: 2017-09-09 23:00:00
ℹ Pressure: 876 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 51 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 11
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 8
ℹ Date: 2017-09-10 00:00:00
ℹ Pressure: 851 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 26 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 11
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 8
ℹ Date: 2017-09-10 01:00:00
ℹ Pressure: 966 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 141 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 11
ℹ Flight index: 1 of 1
ℹ Time index: 8 of 8
ℹ Date: 2017-09-10 02:00:00
ℹ Pressure: 980 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 155 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 12
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 10
ℹ Date: 2017-09-10 19:00:00
ℹ Pressure: 979 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 104 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 12
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 10
ℹ Date: 2017-09-10 20:00:00
ℹ Pressure: 917 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 42 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 12
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 10
ℹ Date: 2017-09-10 21:00:00
ℹ Pressure: 935 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 60 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 12
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 10
ℹ Date: 2017-09-10 22:00:00
ℹ Pressure: 963 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 88 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 12
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 10
ℹ Date: 2017-09-10 23:00:00
ℹ Pressure: 958 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 83 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 12
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 10
ℹ Date: 2017-09-11 00:00:00
ℹ Pressure: 940 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 65 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 12
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 10
ℹ Date: 2017-09-11 01:00:00
ℹ Pressure: 923 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 48 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 12
ℹ Flight index: 1 of 1
ℹ Time index: 8 of 10
ℹ Date: 2017-09-11 02:00:00
ℹ Pressure: 886 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 11 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 12
ℹ Flight index: 1 of 1
ℹ Time index: 9 of 10
ℹ Date: 2017-09-11 03:00:00
ℹ Pressure: 997 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 122 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 12
ℹ Flight index: 1 of 1
ℹ Time index: 10 of 10
ℹ Date: 2017-09-11 04:00:00
ℹ Pressure: 998 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 123 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 13
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 3
ℹ Date: 2017-09-11 23:00:00
ℹ Pressure: 997 hPa
ℹ Highest available level: 975 hPa
ℹ Pressure difference: 22 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 13
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 3
ℹ Date: 2017-09-12 00:00:00
ℹ Pressure: 988 hPa
ℹ Highest available level: 975 hPa
ℹ Pressure difference: 13 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 13
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 3
ℹ Date: 2017-09-12 01:00:00
ℹ Pressure: 997 hPa
ℹ Highest available level: 975 hPa
ℹ Pressure difference: 22 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 14
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 10
ℹ Date: 2017-09-15 20:00:00
ℹ Pressure: 996 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 221 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 14
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 10
ℹ Date: 2017-09-15 21:00:00
ℹ Pressure: 978 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 203 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 14
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 10
ℹ Date: 2017-09-15 22:00:00
ℹ Pressure: 838 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 63 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 14
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 10
ℹ Date: 2017-09-15 23:00:00
ℹ Pressure: 817 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 42 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 14
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 10
ℹ Date: 2017-09-16 00:00:00
ℹ Pressure: 787 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 12 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 14
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 10
ℹ Date: 2017-09-16 01:00:00
ℹ Pressure: 791 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 16 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 14
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 10
ℹ Date: 2017-09-16 02:00:00
ℹ Pressure: 786 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 11 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 14
ℹ Flight index: 1 of 1
ℹ Time index: 8 of 10
ℹ Date: 2017-09-16 03:00:00
ℹ Pressure: 816 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 41 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 14
ℹ Flight index: 1 of 1
ℹ Time index: 9 of 10
ℹ Date: 2017-09-16 04:00:00
ℹ Pressure: 897 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 122 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 14
ℹ Flight index: 1 of 1
ℹ Time index: 10 of 10
ℹ Date: 2017-09-16 05:00:00
ℹ Pressure: 982 hPa
ℹ Highest available level: 775 hPa
ℹ Pressure difference: 207 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 15
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 7
ℹ Date: 2017-09-16 20:00:00
ℹ Pressure: 983 hPa
ℹ Highest available level: 925 hPa
ℹ Pressure difference: 58 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 15
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 7
ℹ Date: 2017-09-16 21:00:00
ℹ Pressure: 959 hPa
ℹ Highest available level: 925 hPa
ℹ Pressure difference: 34 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 15
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 7
ℹ Date: 2017-09-16 22:00:00
ℹ Pressure: 948 hPa
ℹ Highest available level: 925 hPa
ℹ Pressure difference: 23 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 15
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 7
ℹ Date: 2017-09-16 23:00:00
ℹ Pressure: 980 hPa
ℹ Highest available level: 925 hPa
ℹ Pressure difference: 55 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 15
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 7
ℹ Date: 2017-09-17 00:00:00
ℹ Pressure: 980 hPa
ℹ Highest available level: 925 hPa
ℹ Pressure difference: 55 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 15
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 7
ℹ Date: 2017-09-17 01:00:00
ℹ Pressure: 972 hPa
ℹ Highest available level: 925 hPa
ℹ Pressure difference: 47 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 15
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 7
ℹ Date: 2017-09-17 02:00:00
ℹ Pressure: 987 hPa
ℹ Highest available level: 925 hPa
ℹ Pressure difference: 62 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 16
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 6
ℹ Date: 2017-09-18 19:00:00
ℹ Pressure: 988 hPa
ℹ Highest available level: 950 hPa
ℹ Pressure difference: 38 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 16
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 6
ℹ Date: 2017-09-18 20:00:00
ℹ Pressure: 974 hPa
ℹ Highest available level: 950 hPa
ℹ Pressure difference: 24 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 16
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 6
ℹ Date: 2017-09-18 21:00:00
ℹ Pressure: 977 hPa
ℹ Highest available level: 950 hPa
ℹ Pressure difference: 27 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 16
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 6
ℹ Date: 2017-09-18 22:00:00
ℹ Pressure: 973 hPa
ℹ Highest available level: 950 hPa
ℹ Pressure difference: 23 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 16
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 6
ℹ Date: 2017-09-18 23:00:00
ℹ Pressure: 983 hPa
ℹ Highest available level: 950 hPa
ℹ Pressure difference: 33 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 16
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 6
ℹ Date: 2017-09-19 00:00:00
ℹ Pressure: 997 hPa
ℹ Highest available level: 950 hPa
ℹ Pressure difference: 47 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 17
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 4
ℹ Date: 2017-09-19 23:00:00
ℹ Pressure: 995 hPa
ℹ Highest available level: 975 hPa
ℹ Pressure difference: 20 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 17
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 4
ℹ Date: 2017-09-20 00:00:00
ℹ Pressure: 993 hPa
ℹ Highest available level: 975 hPa
ℹ Pressure difference: 18 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 17
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 4
ℹ Date: 2017-09-20 01:00:00
ℹ Pressure: 990 hPa
ℹ Highest available level: 975 hPa
ℹ Pressure difference: 15 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 17
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 4
ℹ Date: 2017-09-20 02:00:00
ℹ Pressure: 996 hPa
ℹ Highest available level: 975 hPa
ℹ Pressure difference: 21 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 18
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 13
ℹ Date: 2017-12-05 18:00:00
ℹ Pressure: 995 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 170 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 18
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 13
ℹ Date: 2017-12-05 19:00:00
ℹ Pressure: 982 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 157 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 18
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 13
ℹ Date: 2017-12-05 20:00:00
ℹ Pressure: 960 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 135 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 18
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 13
ℹ Date: 2017-12-05 21:00:00
ℹ Pressure: 942 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 117 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 18
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 13
ℹ Date: 2017-12-05 22:00:00
ℹ Pressure: 951 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 126 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 18
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 13
ℹ Date: 2017-12-05 23:00:00
ℹ Pressure: 906 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 81 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 18
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 13
ℹ Date: 2017-12-06 00:00:00
ℹ Pressure: 881 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 56 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 18
ℹ Flight index: 1 of 1
ℹ Time index: 8 of 13
ℹ Date: 2017-12-06 01:00:00
ℹ Pressure: 919 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 94 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 18
ℹ Flight index: 1 of 1
ℹ Time index: 9 of 13
ℹ Date: 2017-12-06 02:00:00
ℹ Pressure: 877 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 52 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 18
ℹ Flight index: 1 of 1
ℹ Time index: 10 of 13
ℹ Date: 2017-12-06 03:00:00
ℹ Pressure: 836 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 11 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 18
ℹ Flight index: 1 of 1
ℹ Time index: 11 of 13
ℹ Date: 2017-12-06 04:00:00
ℹ Pressure: 860 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 35 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 18
ℹ Flight index: 1 of 1
ℹ Time index: 12 of 13
ℹ Date: 2017-12-06 05:00:00
ℹ Pressure: 871 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 46 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 18
ℹ Flight index: 1 of 1
ℹ Time index: 13 of 13
ℹ Date: 2017-12-06 06:00:00
ℹ Pressure: 978 hPa
ℹ Highest available level: 825 hPa
ℹ Pressure difference: 153 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 19
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 7
ℹ Date: 2017-12-06 19:00:00
ℹ Pressure: 978 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 178 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 19
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 7
ℹ Date: 2017-12-06 20:00:00
ℹ Pressure: 872 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 72 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 19
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 7
ℹ Date: 2017-12-06 21:00:00
ℹ Pressure: 937 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 137 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 19
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 7
ℹ Date: 2017-12-06 22:00:00
ℹ Pressure: 878 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 78 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 19
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 7
ℹ Date: 2017-12-06 23:00:00
ℹ Pressure: 915 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 115 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 19
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 7
ℹ Date: 2017-12-07 00:00:00
ℹ Pressure: 924 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 124 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 19
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 7
ℹ Date: 2017-12-07 01:00:00
ℹ Pressure: 985 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 185 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 20
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 7
ℹ Date: 2018-04-10 19:00:00
ℹ Pressure: 988 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 113 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 20
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 7
ℹ Date: 2018-04-10 20:00:00
ℹ Pressure: 976 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 101 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 20
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 7
ℹ Date: 2018-04-10 21:00:00
ℹ Pressure: 962 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 87 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 20
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 7
ℹ Date: 2018-04-10 22:00:00
ℹ Pressure: 926 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 51 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 20
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 7
ℹ Date: 2018-04-10 23:00:00
ℹ Pressure: 928 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 53 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 20
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 7
ℹ Date: 2018-04-11 00:00:00
ℹ Pressure: 940 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 65 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 20
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 7
ℹ Date: 2018-04-11 01:00:00
ℹ Pressure: 969 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 94 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 21
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 12
ℹ Date: 2018-04-11 19:00:00
ℹ Pressure: 965 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 165 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 21
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 12
ℹ Date: 2018-04-11 20:00:00
ℹ Pressure: 941 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 141 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 21
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 12
ℹ Date: 2018-04-11 21:00:00
ℹ Pressure: 943 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 143 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 21
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 12
ℹ Date: 2018-04-11 22:00:00
ℹ Pressure: 961 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 161 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 21
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 12
ℹ Date: 2018-04-11 23:00:00
ℹ Pressure: 955 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 155 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 21
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 12
ℹ Date: 2018-04-12 00:00:00
ℹ Pressure: 942 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 142 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 21
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 12
ℹ Date: 2018-04-12 01:00:00
ℹ Pressure: 915 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 115 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 21
ℹ Flight index: 1 of 1
ℹ Time index: 8 of 12
ℹ Date: 2018-04-12 02:00:00
ℹ Pressure: 940 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 140 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 21
ℹ Flight index: 1 of 1
ℹ Time index: 9 of 12
ℹ Date: 2018-04-12 03:00:00
ℹ Pressure: 933 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 133 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 21
ℹ Flight index: 1 of 1
ℹ Time index: 10 of 12
ℹ Date: 2018-04-12 04:00:00
ℹ Pressure: 921 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 121 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 21
ℹ Flight index: 1 of 1
ℹ Time index: 11 of 12
ℹ Date: 2018-04-12 05:00:00
ℹ Pressure: 812 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 12 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 21
ℹ Flight index: 1 of 1
ℹ Time index: 12 of 12
ℹ Date: 2018-04-12 06:00:00
ℹ Pressure: 978 hPa
ℹ Highest available level: 800 hPa
ℹ Pressure difference: 178 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 22
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 12
ℹ Date: 2018-04-12 19:00:00
ℹ Pressure: 977 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 277 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 22
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 12
ℹ Date: 2018-04-12 20:00:00
ℹ Pressure: 857 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 157 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 22
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 12
ℹ Date: 2018-04-12 21:00:00
ℹ Pressure: 723 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 23 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 22
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 12
ℹ Date: 2018-04-12 22:00:00
ℹ Pressure: 715 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 15 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 22
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 12
ℹ Date: 2018-04-12 23:00:00
ℹ Pressure: 702 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 2 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 22
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 12
ℹ Date: 2018-04-13 00:00:00
ℹ Pressure: 738 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 38 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 22
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 12
ℹ Date: 2018-04-13 01:00:00
ℹ Pressure: 833 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 133 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 22
ℹ Flight index: 1 of 1
ℹ Time index: 8 of 12
ℹ Date: 2018-04-13 02:00:00
ℹ Pressure: 862 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 162 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 22
ℹ Flight index: 1 of 1
ℹ Time index: 9 of 12
ℹ Date: 2018-04-13 03:00:00
ℹ Pressure: 830 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 130 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 22
ℹ Flight index: 1 of 1
ℹ Time index: 10 of 12
ℹ Date: 2018-04-13 04:00:00
ℹ Pressure: 822 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 122 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 22
ℹ Flight index: 1 of 1
ℹ Time index: 11 of 12
ℹ Date: 2018-04-13 05:00:00
ℹ Pressure: 816 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 116 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 22
ℹ Flight index: 1 of 1
ℹ Time index: 12 of 12
ℹ Date: 2018-04-13 06:00:00
ℹ Pressure: 985 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 285 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 23
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 12
ℹ Date: 2018-04-13 19:00:00
ℹ Pressure: 983 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 383 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 23
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 12
ℹ Date: 2018-04-13 20:00:00
ℹ Pressure: 792 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 192 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 23
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 12
ℹ Date: 2018-04-13 21:00:00
ℹ Pressure: 648 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 48 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 23
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 12
ℹ Date: 2018-04-13 22:00:00
ℹ Pressure: 666 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 66 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 23
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 12
ℹ Date: 2018-04-13 23:00:00
ℹ Pressure: 692 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 92 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 23
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 12
ℹ Date: 2018-04-14 00:00:00
ℹ Pressure: 721 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 121 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 23
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 12
ℹ Date: 2018-04-14 01:00:00
ℹ Pressure: 714 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 114 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 23
ℹ Flight index: 1 of 1
ℹ Time index: 8 of 12
ℹ Date: 2018-04-14 02:00:00
ℹ Pressure: 708 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 108 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 23
ℹ Flight index: 1 of 1
ℹ Time index: 9 of 12
ℹ Date: 2018-04-14 03:00:00
ℹ Pressure: 672 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 72 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 23
ℹ Flight index: 1 of 1
ℹ Time index: 10 of 12
ℹ Date: 2018-04-14 04:00:00
ℹ Pressure: 659 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 59 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 23
ℹ Flight index: 1 of 1
ℹ Time index: 11 of 12
ℹ Date: 2018-04-14 05:00:00
ℹ Pressure: 662 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 62 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 23
ℹ Flight index: 1 of 1
ℹ Time index: 12 of 12
ℹ Date: 2018-04-14 06:00:00
ℹ Pressure: 957 hPa
ℹ Highest available level: 600 hPa
ℹ Pressure difference: 357 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 23
ℹ Date: 2018-04-14 18:00:00
ℹ Pressure: 957 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 457 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 23
ℹ Date: 2018-04-14 19:00:00
ℹ Pressure: 834 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 334 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 23
ℹ Date: 2018-04-14 20:00:00
ℹ Pressure: 757 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 257 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 23
ℹ Date: 2018-04-14 21:00:00
ℹ Pressure: 731 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 231 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 23
ℹ Date: 2018-04-14 22:00:00
ℹ Pressure: 743 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 243 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 23
ℹ Date: 2018-04-14 23:00:00
ℹ Pressure: 749 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 249 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 23
ℹ Date: 2018-04-15 00:00:00
ℹ Pressure: 697 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 197 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 8 of 23
ℹ Date: 2018-04-15 01:00:00
ℹ Pressure: 652 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 152 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 9 of 23
ℹ Date: 2018-04-15 02:00:00
ℹ Pressure: 617 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 117 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 10 of 23
ℹ Date: 2018-04-15 03:00:00
ℹ Pressure: 631 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 131 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 11 of 23
ℹ Date: 2018-04-15 04:00:00
ℹ Pressure: 601 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 101 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 12 of 23
ℹ Date: 2018-04-15 05:00:00
ℹ Pressure: 617 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 117 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 13 of 23
ℹ Date: 2018-04-15 06:00:00
ℹ Pressure: 544 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 44 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 14 of 23
ℹ Date: 2018-04-15 07:00:00
ℹ Pressure: 537 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 37 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 15 of 23
ℹ Date: 2018-04-15 08:00:00
ℹ Pressure: 525 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 25 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 16 of 23
ℹ Date: 2018-04-15 09:00:00
ℹ Pressure: 519 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 19 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 17 of 23
ℹ Date: 2018-04-15 10:00:00
ℹ Pressure: 518 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 18 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 18 of 23
ℹ Date: 2018-04-15 11:00:00
ℹ Pressure: 514 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 14 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 19 of 23
ℹ Date: 2018-04-15 12:00:00
ℹ Pressure: 539 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 39 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 20 of 23
ℹ Date: 2018-04-15 13:00:00
ℹ Pressure: 541 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 41 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 21 of 23
ℹ Date: 2018-04-15 14:00:00
ℹ Pressure: 543 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 43 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 22 of 23
ℹ Date: 2018-04-15 15:00:00
ℹ Pressure: 662 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 162 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 24
ℹ Flight index: 1 of 1
ℹ Time index: 23 of 23
ℹ Date: 2018-04-15 16:00:00
ℹ Pressure: 896 hPa
ℹ Highest available level: 500 hPa
ℹ Pressure difference: 396 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 25
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 6
ℹ Date: 2018-04-15 18:00:00
ℹ Pressure: 895 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 20 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 25
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 6
ℹ Date: 2018-04-15 19:00:00
ℹ Pressure: 923 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 48 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 25
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 6
ℹ Date: 2018-04-15 20:00:00
ℹ Pressure: 1002 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 127 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 25
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 6
ℹ Date: 2018-04-15 21:00:00
ℹ Pressure: 892 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 17 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 25
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 6
ℹ Date: 2018-04-15 22:00:00
ℹ Pressure: 1003 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 128 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 25
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 6
ℹ Date: 2018-04-15 23:00:00
ℹ Pressure: 1009 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 134 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 26
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 10
ℹ Date: 2018-04-25 18:00:00
ℹ Pressure: 1018 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 143 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 26
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 10
ℹ Date: 2018-04-25 19:00:00
ℹ Pressure: 977 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 102 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 26
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 10
ℹ Date: 2018-04-25 20:00:00
ℹ Pressure: 972 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 97 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 26
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 10
ℹ Date: 2018-04-25 21:00:00
ℹ Pressure: 924 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 49 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 26
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 10
ℹ Date: 2018-04-25 22:00:00
ℹ Pressure: 961 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 86 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 26
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 10
ℹ Date: 2018-04-25 23:00:00
ℹ Pressure: 918 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 43 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 26
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 10
ℹ Date: 2018-04-26 00:00:00
ℹ Pressure: 919 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 44 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 26
ℹ Flight index: 1 of 1
ℹ Time index: 8 of 10
ℹ Date: 2018-04-26 01:00:00
ℹ Pressure: 877 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 2 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 26
ℹ Flight index: 1 of 1
ℹ Time index: 9 of 10
ℹ Date: 2018-04-26 02:00:00
ℹ Pressure: 891 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 16 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 26
ℹ Flight index: 1 of 1
ℹ Time index: 10 of 10
ℹ Date: 2018-04-26 03:00:00
ℹ Pressure: 1009 hPa
ℹ Highest available level: 875 hPa
ℹ Pressure difference: 134 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 27
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 8
ℹ Date: 2018-04-29 21:00:00
ℹ Pressure: 1007 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 307 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 27
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 8
ℹ Date: 2018-04-29 22:00:00
ℹ Pressure: 854 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 154 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 27
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 8
ℹ Date: 2018-04-29 23:00:00
ℹ Pressure: 815 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 115 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 27
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 8
ℹ Date: 2018-04-30 00:00:00
ℹ Pressure: 902 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 202 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 27
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 8
ℹ Date: 2018-04-30 01:00:00
ℹ Pressure: 856 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 156 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 27
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 8
ℹ Date: 2018-04-30 02:00:00
ℹ Pressure: 720 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 20 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 27
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 8
ℹ Date: 2018-04-30 03:00:00
ℹ Pressure: 914 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 214 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 27
ℹ Flight index: 1 of 1
ℹ Time index: 8 of 8
ℹ Date: 2018-04-30 04:00:00
ℹ Pressure: 1001 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 301 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 28
ℹ Flight index: 1 of 1
ℹ Time index: 1 of 9
ℹ Date: 2018-04-30 18:00:00
ℹ Pressure: 1001 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 301 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 28
ℹ Flight index: 1 of 1
ℹ Time index: 2 of 9
ℹ Date: 2018-04-30 19:00:00
ℹ Pressure: 946 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 246 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 28
ℹ Flight index: 1 of 1
ℹ Time index: 3 of 9
ℹ Date: 2018-04-30 20:00:00
ℹ Pressure: 813 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 113 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 28
ℹ Flight index: 1 of 1
ℹ Time index: 4 of 9
ℹ Date: 2018-04-30 21:00:00
ℹ Pressure: 740 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 40 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 28
ℹ Flight index: 1 of 1
ℹ Time index: 5 of 9
ℹ Date: 2018-04-30 22:00:00
ℹ Pressure: 905 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 205 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 28
ℹ Flight index: 1 of 1
ℹ Time index: 6 of 9
ℹ Date: 2018-04-30 23:00:00
ℹ Pressure: 976 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 276 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 28
ℹ Flight index: 1 of 1
ℹ Time index: 7 of 9
ℹ Date: 2018-05-01 00:00:00
ℹ Pressure: 957 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 257 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 28
ℹ Flight index: 1 of 1
ℹ Time index: 8 of 9
ℹ Date: 2018-05-01 01:00:00
ℹ Pressure: 979 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 279 hPa

Warning: ! Pressure is above the highest level while the highest level is not 1000hPa.
ℹ Stationary period: 28
ℹ Flight index: 1 of 1
ℹ Time index: 9 of 9
ℹ Date: 2018-05-01 02:00:00
ℹ Pressure: 990 hPa
ℹ Highest available level: 700 hPa
ℹ Pressure difference: 290 hPa

ℹ Pruning the graph: 0/54 transitions (forward and backward).

ℹ Pruning the graph: 10/54 transitions (forward and backward).

✔ Graph pruned [853ms]

5.4 Define movement model

While you can still define the movement model with a parametric function (i.e., gamma or logit), we find it more intuitive to use the mechanical power curve. The power curve expresses the energy required for a bird to fly at a certain airspeed based on aerodynamic theory. See more details in section 2.2.5 of Nussbaumer et al. (2023).

First, we search for morphological information on the Great Reed Warbler using the AVONET database (Tobias et al. 2022).

bird <- bird_create("Acrocephalus arundinaceus")

Using the bird created, we can set the movement model by converting the airspeed to power, and power to a probability. This second step is still a parametric equation, which can be manually defined with power2prob.

graph <- graph_set_movement(
  graph,
  method = "power",
  bird = bird,
  power2prob = \(power) (1 / power)^3,
  low_speed_fix = 15
)
plot_graph_movement(graph)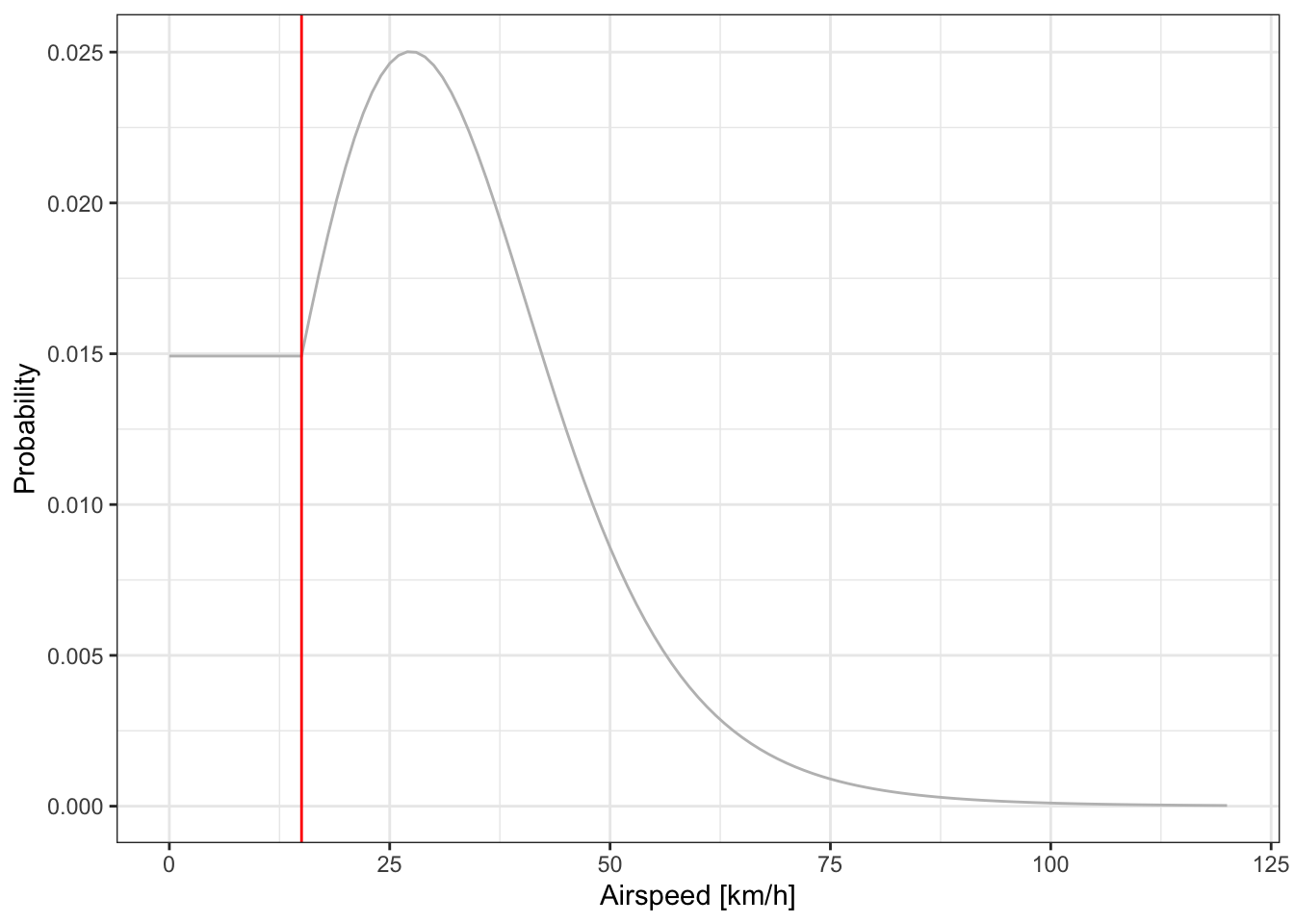

5.5 Products

We can then compute the same three products as for the Swainson’s Warbler:

path_most_likely <- graph_most_likely(graph, quiet = TRUE)
marginal <- graph_marginal(graph, quiet = TRUE)
path_simulation <- graph_simulation(graph, nj = 10, quiet = TRUE)

plot(marginal, path = path_most_likely)

plot_path(path_simulation, plot_leaflet = FALSE)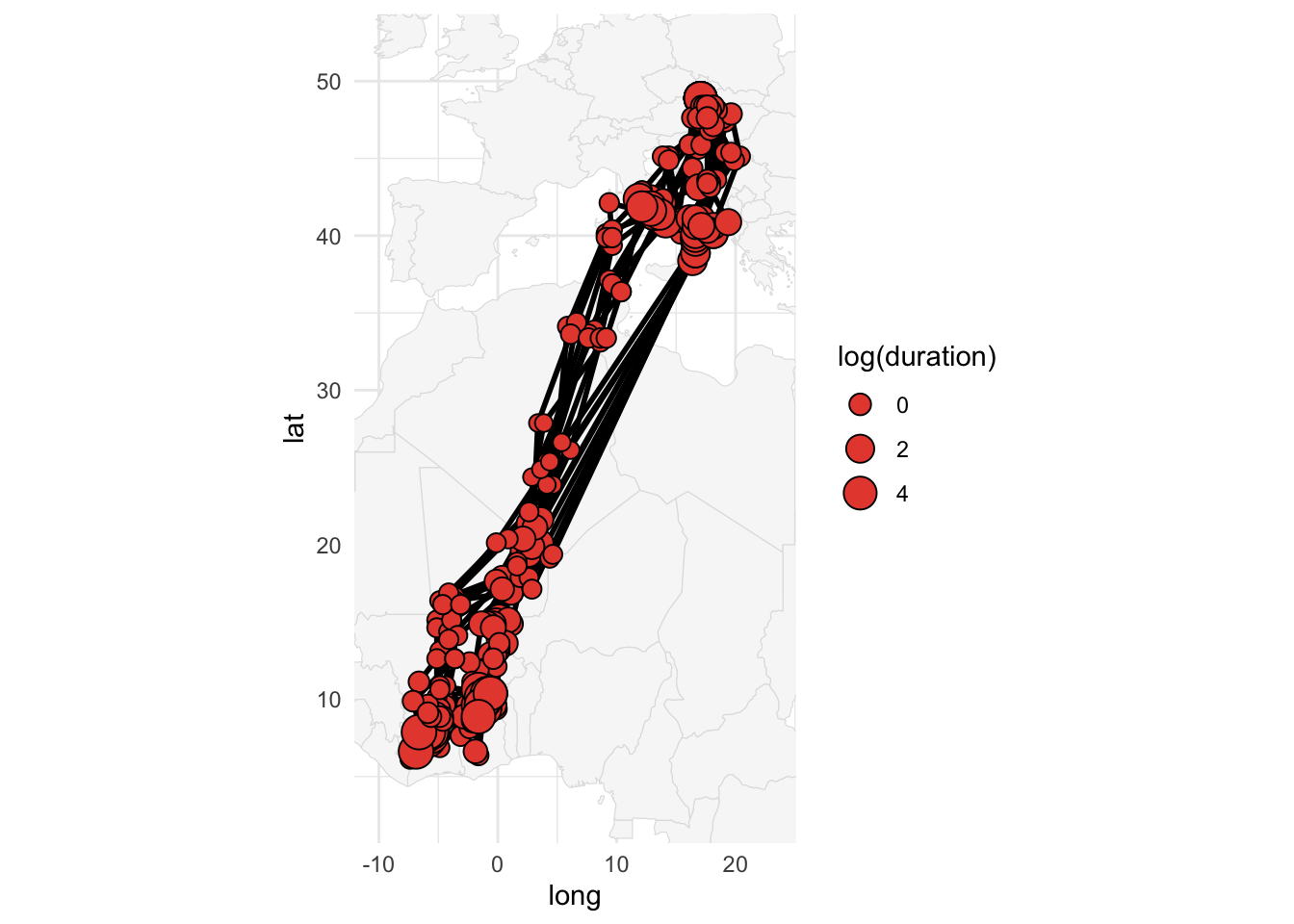

5.5.1 Extract flight information

The pathvariable contains all the information at the scale of the stationary period. However, to get flight information, you need to extract variable of the edge of the graph. path2edge() is the function for that!

edge_simulation <- path2edge(path_simulation, graph)
edge_most_likely <- path2edge(path_most_likely, graph)
knitr::kable(head(edge_most_likely, 3), digits = 1)

	stap_s	stap_t	j	s	t	lat_s	lat_t	lon_s	lon_t	start	end	duration	n	distance	bearing	gs	ws
1	1	2	1	26405	57010	48.9	47.6	17.0	16.4	2017-08-04 19:47:30	2017-08-04 23:17:30	3.5	1	150.4	199.7	-16.1-39.7i	13.8-13.6i
12	2	3	1	57010	86621	47.6	44.9	16.4	14.4	2017-08-05 19:27:30	2017-08-06 02:52:30	7.4	1	342.4	207.5	-21.3-41.0i	-5.5-4.6i
22	3	4	1	86621	118434	44.9	41.6	14.4	15.1	2017-08-06 19:12:30	2017-08-07 03:17:30	8.1	1	366.2	170.2	7.7-44.7i	-7.8-20.6i

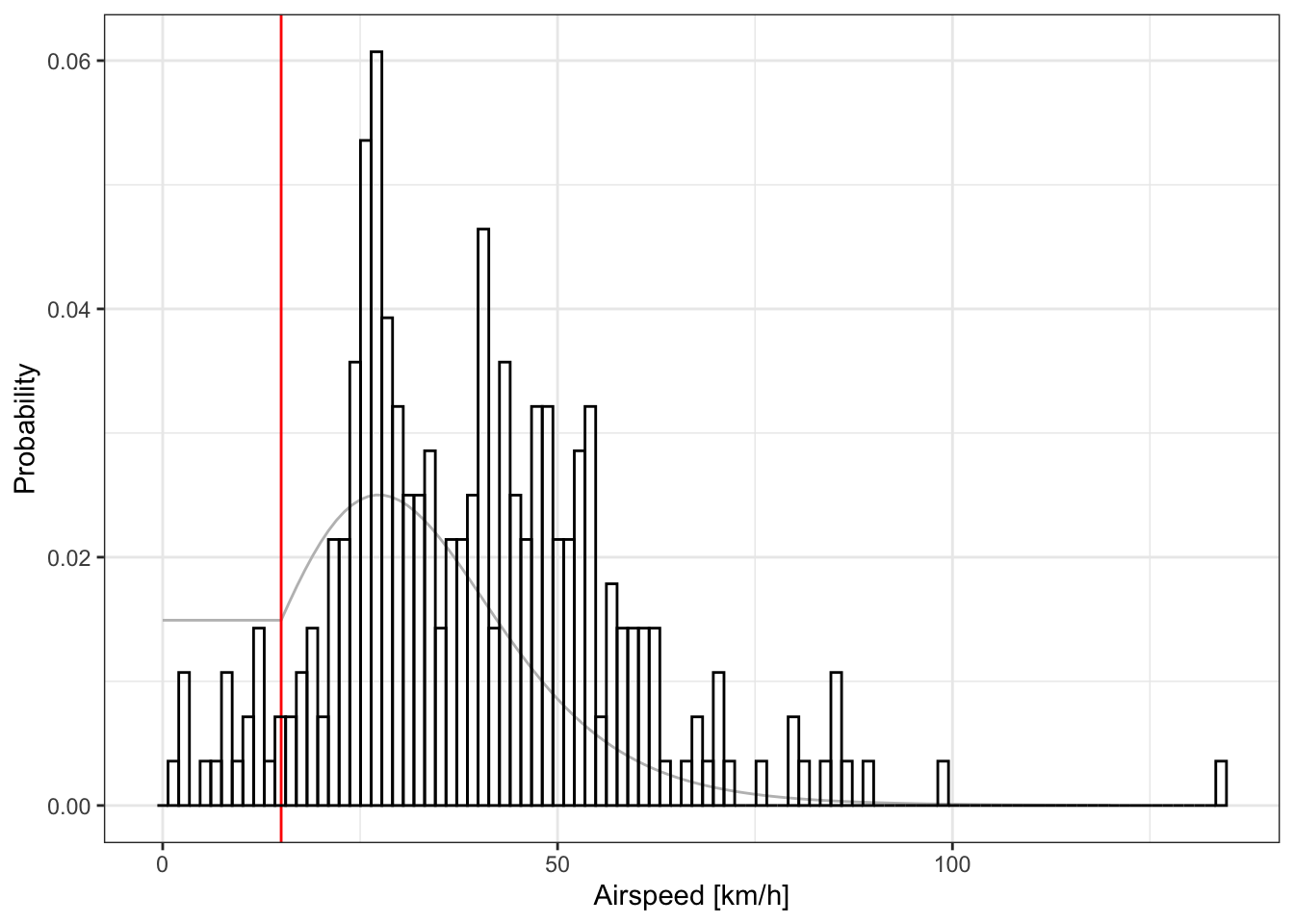
It’s a good idea to check the distribution of ground speed (gs), winspeed (ws) and airspeed (as) and check for any outliers which might come from error in the labelling. Here you can see the high groundspeed (>100km/h between stap 24 and 25) which is nicely explained by wind, as the corresponding airspeed is perfectly normal (~50km/h)

We can (and should) also check that our movement model is coherent with the distribution of flight speed assumed in the movement model:

plot_graph_movement(graph) +
  geom_histogram(
    data = data.frame(as = abs(edge_simulation$gs - edge_simulation$ws)),
    aes(x = as, y = after_stat(count) / sum(after_stat(count))),
    color = "black",
    fill = NA,
    bins = 100
  )

If you find anomalous flight speed, it might be worth checking if this/these flight(s) have been correctly labelled.

5.6 Save

graph can become extremely big for such models and it might not be recommended to save it. Check its size with format(object.size(graph), units = "MB").

save(
  tag,
  graph,
  path_most_likely,
  path_simulation,
  marginal,
  edge_simulation,
  edge_most_likely,
  file = "./data/interim/18LX.RData"
)

Copernicus Climate Change Service. 2018. “ERA5 Hourly Data on Pressure Levels from 1940 to Present.” Copernicus Climate Change Service (C3S) Climate Data Store (CDS). https://doi.org/10.24381/CDS.BD0915C6.

Nussbaumer, Raphaël, Mathieu Gravey, Martins Briedis, Felix Liechti, and Daniel Sheldon. 2023. “Reconstructing Bird Trajectories from Pressure and Wind Data Using a Highly Optimized Hidden Markov Model.” Methods in Ecology and Evolution 14 (4): 1118–29. https://doi.org/10.1111/2041-210X.14082.

Tobias, Joseph A., Catherine Sheard, Alex L. Pigot, Adam J. M. Devenish, Jingyi Yang, Ferran Sayol, Montague H. C. Neate-Clegg, et al. 2022. “AVONET: Morphological, Ecological and Geographical Data for All Birds.” Edited by Tim Coulson. Ecology Letters 25 (3): 581–97. https://doi.org/10.1111/ele.13898.